Eindige Element Analise en Optimalisering Ontwerp van Transmissie Torings

abstrakte:

Hierdie vraestel gebruik die eindige element optimeringsanalise metode en die ANSYS sagteware analise platform om eindige element analise en optimeringsontwerp op die transmissie toring struktuur (neem die staalpyptoring as voorbeeld). In die strukturele analise, gebaseer op die APDL-taal, 'n parametriese eindige element model word gebruik om eindige element analise uit te voer op die meganiese gedrag van die aanvanklike ontwerpskema onder verskeie werksomstandighede, en die meganiese eienskappe van die struktuur onder verskillende werksomstandighede word geëvalueer. Op hierdie basis, die optimaliseringsontwerp word ingestel om die aanvanklike ontwerpskema te optimaliseer. Onder die veronderstelling om aan die sterktemaatstaf te voldoen, die totale massa van die struktuur word geoptimaliseer en verminder met 30%. Daarbenewens, hierdie vraestel stel ook 'n algemene idee van toringontwerp voor: empiriese ontwerp - eindige element strukturele analise - optimalisering ontwerp, wat ontwerpdoeltreffendheid verbeter en koste bespaar, en kan 'n verwysing verskaf vir die oplossing van soortgelyke ingenieursprobleme. sleutelwoorde: eindige element analise; parametriese ontwerp; transmissie toring; strukturele optimalisering ontwerp.

Navorsingsagtergrond

Transmissietorings is belangrike draende strukture in kragoordragtoerusting. Hul veiligheid en stabiliteit sal die gladde werking van die hele kragstelsel direk beïnvloed [1]. Die vragte op transmissietorings is ook kompleks en divers. Gewoonlik, die hoofladings sluit die dooie gewig van die geleiers in, windkrag, en ys. Onder die koppeling van hierdie verskillende vragte, die torings moet voldoende meganiese sterkte hê om die normale werking van die transmissiestelsel te verseker [2]. Moderne hoëvlak transmissielyne wat deur ultrahoëspanning transmissie verteenwoordig word, het toenemend hoër vereistes vir die meganiese eienskappe en veiligheid van torings. daarom, dit is van groot praktiese belang om strukturele sterkte-analise op transmissietorings uit te voer om ernstige skade aan die torings te vermy. Statiese meganiese ontleding van torings is die basis vir die bestudering van hul meganiese eienskappe. Die tradisionele toringstruktuurontwerpmetode is empiriese ontwerp, dit is, die ontwerper ontwerp eers 'n aanvanklike skema volgens relevante vereistes, en kontroleer dan die struktuur met die hand. As dit nie aan die vereistes van meganiese eienskappe voldoen nie, die struktuur word weer gewysig en weer nagegaan, en hierdie proses word herhaal totdat die finale ontwerpskema verkry is. Hierdie ontwerpmetode is ondoeltreffend, tydrowend, en hoogs afhanklik van die ervaringsvlak van die ontwerper. Hierdie metode is selfs moeiliker om te werk in die lig van toenemend komplekse en diverse strukture van transmissietorings. Met die ontwikkeling van moderne rekenaarmeganika, eindige element simulasie analise het die akkuraatheid en doeltreffendheid van analise aansienlik verbeter. Hierdie vraestel kies ANSYS-sagteware as die ontledingsplatform om eindige-element-analise en optimeringsontwerp op transmissietorings uit te voer.

1 Eindige Element Analise van Transmissietoringstruktuur

1.1 Navorsingsobjek
Daar is baie soorte transmissietoringstrukture. Hierdie vraestel beoog om die struktuur van 'n nuwer tipe transmissietoringstruktuur te ontleed, die vier-buis staal pyp toring. Hierdie toring is 'n 220kV enkelkring 50° hoek staal pyp toring. Sy hoof- en dwarsbalke is van staalpype gemaak. Die toring is 50m hoog, en die posisie en breedte van die drie dwarsarms in die hoogte rigting is bekend. Daarbenewens, alle ander inligting is onseker, soos die spasiëring van dwarsbalke, die spasiëring van dwarsarmstutstawe, materiaal parameters, belangrikste materiale, dwarsbalke, en hoek staal deursnee afmetings. In die lig van hierdie situasie, empiriese ontwerp moet eers uitgevoer word om die basiese vorm van die toring te bepaal, verkry die aanvanklike ontwerpskema, en voer dan eindige element-analise op hierdie skema uit. Voordat eindige element analise uitgevoer word, dit is nodig om die struktuur te vereenvoudig en slegs eindige element analise uit te voer op die komponente wat die hoof meganiese eienskappe van die struktuur weerspieël. Byvoorbeeld, in die transmissietoring, die verbindingsboute, verbindingsplate en aanhegsels kan eers geïgnoreer word, en die toringraam kan ontleed word, wat nie net op die stresgedrag van die struktuur kan fokus nie, maar vermy ook om te veel rekenaarhulpbronne te vermors.

1.2 Meetkundige modellering
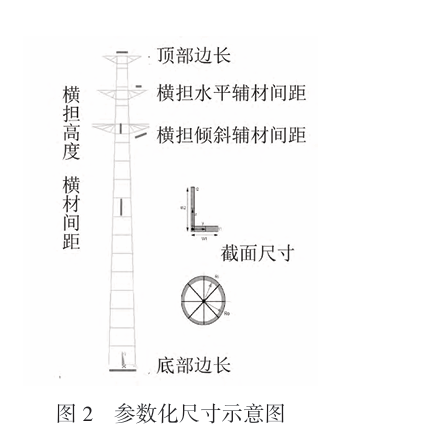
Sodra die vaste parameters ingevoer is, die geometriese vorm en hoof meganiese parameters van die eindige element model is basies vas. Dit word hoofsaaklik gebruik vir meganiese ontleding van gestelde parameters, en kan nie vir die optimalisering van sleutelontwerpveranderlikes gebruik word nie. Die universaliteit is swak. Hierdie vraestel fokus op die optimalisering van die hoofontwerpparameters van die transmissietoring. daarom, dit is nodig om die parametriese eindige element modellering metode aan te neem. Volgens die idee van parametriese modellering, gebaseer op die APDL-taal, die hele toringstruktuurmodule is in vier dele in die geometriese struktuur verdeel: belangrikste materiaal, kruis materiaal, kruisarmplaat en kruisarmhulpmateriaal. Die meetkundige model word op sy beurt gevestig, en uiteindelik word die algehele model verkry deur “algemene vergadering”. Die skematiese diagram van modulêre modellering word in Figuur getoon 1. In die modelleringsproses van hierdie vraestel, sommige meetkundige afmetings is geparameteriseer, soos kruisarmhoogte, dwarsbalkspasiëring, bokant lengte, horisontale kruisarm hulpmateriaal spasiëring, skuins dwarsarm hulpmateriaal spasiëring en deursnee afmetings. Die skematiese diagram van geparameteriseerde afmetings word in Figuur getoon 2. In die aanvanklike ontwerpskema, alle staalmateriaal is ingestel op Q235-staal met 'n vloeisterkte van 235MPa. Die eindige element sagteware self voer slegs numeriese berekeninge uit. In terme van eenheidstelsel, die gebruiker kan self 'n geslote eenheidstelsel instel. Vir gerief, hierdie vraestel gebruik die mm-ton-N-MPa-eenheidstelsel in ontleding.

1.3 Maas verdeling

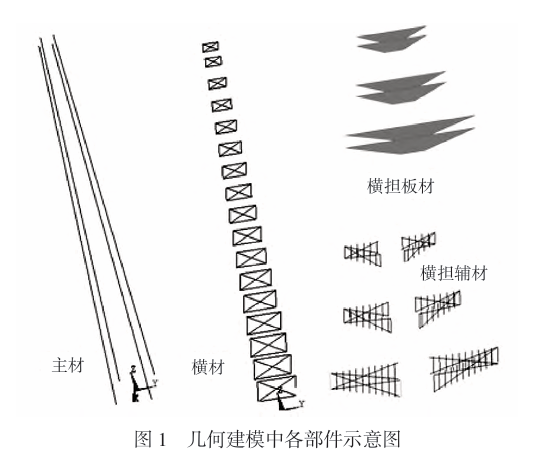
Die transmissietoringstruktuur het baie verbindingsvorme, en die deursneevorms van die komponente is uiteenlopend, en die oriëntasie en algehele strestoestande is relatief kompleks. Die konvensionele eindige element analise model vereenvoudig die toring in 'n ruimtelike truss model. Die hoofprobleme is soos volg: Eerste, slegs die aksiale spanning en kompressie van die hoofmateriaal word oorweeg, maar in werklikheid, bykomend tot aksiale spanning en kompressie, die hoofmateriaal van die toring dra ook komplekse buigmomente en wringkragte. tweede, by die nodusverbinding, die vereenvoudigde skarnier kan nie buigmoment oordra nie. Die werklike toringverbinding word gewoonlik deur boute verbind, sweiswerk, ens. Die spesifieke rigiede verbindingskenmerke is daardie buigmoment, skeer, ens. kan by die verbinding versend word, terwyl die vereenvoudigde skarnier nie die werklike rigiede verbinding ten volle kan weerspieël nie. derde, die model kan nie die dwarssnitspanning van die komponent ten volle vertoon nie, en vertoon gewoonlik net die nodusspanning van die eindige elementmodel. Volgens die spanningseienskappe van die transmissietoring, hierdie artikel kyk na die komplekse gevolge van spanning, kompressie, buig, en torsie op die stawe, en gebruik 3D-balkelemente (balk189) vir modellering. Op dieselfde tyd, die verskille in die deursnee vorm en oriëntasie van elke staaf word oorweeg, en die deursnee vorm en rigting word gedefinieer. In die na-verwerking van die eindige element analise resultate, die dwarssnitspanning word onttrek, nie net die nodusspanning nie. Met inagneming van die komplekse spanningstoestande van die dwarsarmplaat, die dopelement (dop63) word gebruik vir meshing. Die 3D balk eenheid-dop eenheid eindige element analise model in hierdie vraestel kan die probleme van die truss model vermy, weerspieël die komplekse spanningstoestande van die hoofmateriale en die rigiede verbinding van die verbindingspunte, weerspieël die deursneevorm van die komponente volledig en vertoon die dwarssnitspanning van die komponente, en kan die algehele spanningseienskappe van die transmissietoring ten volle weerspieël.

1.4 Grensvoorwaardes

Die vragte wat deur die transmissietoring gedra word, is relatief kompleks, hoofsaaklik selfgewig ingesluit, windlading, die effek van die geleier op die toring, en aanhangsels (yslaag, hardeware, ens.). Daarbenewens, spesiale situasies soos lynbreuk moet in ag geneem word. In die ontwerp van die toring, die berekening van vragte is relatief volwasse, en daar is baie spesiale berekeningsprogramme wat die spanningstoestande van die toring onder verskeie werkstoestande en meteorologiese toestande kan bereken, en dan gelykstaande aan die relevante punte van die toring. Hierdie vraestel gebruik die “MYLHZ volle spanning las berekening stelsel” om die spanningstoestande van die toring onder verskeie werksomstandighede te bereken. Daar moet kennis geneem word dat hierdie program die strestoestande van honderde werksomstandighede kan bereken. Na voorlopige empiriese ontleding, hierdie vraestel uiteindelik gekies 5 relatief ernstige werksomstandighede vir gedetailleerde ontleding. Hierdie 5 werksomstandighede is soos volg. Werkende toestand 13: sterk wind, ongebalanseerde spanning, 0-graad wind; werkende toestand 16: sterk wind, ongebalanseerde spanning, 90-graad wind; werkende toestand 25: ysbedekking, gebalanseerde spanning, 0-graad wind; werkende toestand 78: gebreekte draad, ongebalanseerde spanning, geen wind nie, gebreekte geleier, 1, 3; werkende toestand 87: installasie, aangrensende rat nie gehang nie, 90-graad wind, traksie geleier 1. Relatiewe krag randvoorwaardes, die verplasingsbeperking van die toring is relatief eenvoudig, dit is, die onderkant 4 punte is ten volle beperk.

1.5 Analise en bespreking van eindige element model resultate

Hierdie vraestel is hoofsaaklik gebaseer op die sterkte-kriterium wanneer eindige-elementontleding op die aanvanklike skema uitgevoer word, dit is, die maksimum ekwivalente spanning van die struktuur kan nie die vloeigrens oorskry nie. In hierdie geval, die struktuur word as veilig beskou, anders word geag dat die moontlikheid van strukturele mislukking hoog is. Na ontleding, daar is gevind dat onder werkende toestand 25, die maksimum verplasing van die toring het 384mm bereik en die maksimum ekwivalente spanning was 330MPa, wat die opbrengswaarde van die materiaal 235MPa oorskry het. daarom, die moontlikheid van strukturele mislukking onder hierdie werkstoestand is relatief hoog. Sien Figuur 3 vir besonderhede.

2 Optimaliseringsontwerp van transmissietoringstruktuur

2.1 Inleiding tot optimeringsontwerp
Optimeringsontwerp is 'n tegniek om die optimale ontwerpoplossing te vind, wat is om die optimale ontwerpoplossing te vind wat die ontwerpdoelwit onder die beperkings kan bereik. Die internasionale grootskaalse sagteware ANSYS bied 'n optimeringsontwerpmodule en alle geparameteriseerde ANSYS-opsies kan vir optimeringsontwerp gebruik word. Die hoofberekeningsproses van optimaliseringsontwerp is soos volg: eers, inisialiseer die veranderlikes en vestig 'n parametriese model. Toe, volgens die objektiewe funksie en beperkings, kombineer die ontwerpveranderlikes om eindige-elementberekening en -analise uit te voer, gebruik die nul-orde optimeringsmetode om globale soektog en optimering uit te voer, en beoordeel dan die konvergensie van die resultate. As konvergensie, die berekening eindig en die optimeringsresultaat word verkry; indien nie, pas die ontwerpveranderlikes aan en herbereken tot konvergensie..

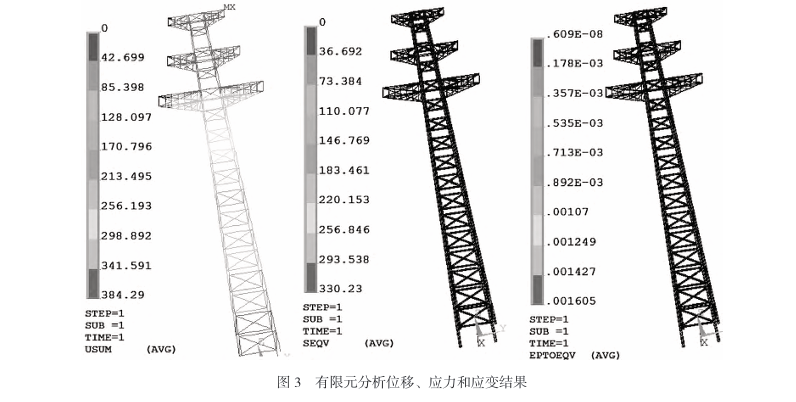
2.2 Opstel van optimeringsparameters
Volgens die basiese idee van optimaliseringsontwerp, die drie sleutelpunte van optimeringsontwerp sluit die keuse van ontwerpveranderlikes in, beperkings en objektiewe funksies. Sedert die basiese vorm van die toring struktuur is bepaal, maar daar is nog baie parameters wat ontwerp kan word, sommige sleutelparameters word gekies vir optimalisering. Hierdie vraestel kies 16 veranderlikes soos lengte van die onderkant, bokant lengte, dwarsbalkspasiëring, en deursnee-afmetings as ontwerpveranderlikes. Die optimalisering is gebaseer op die sterktekriterium, dus is die beperking seleksie relatief eenvoudig, dit is, die maksimum deursneespanning van verskeie eenhede kan nie die vloeisterkte van 235MPa oorskry nie.

2.3   Objektiewe funksie seleksie
Aanvanklike struktuur
Die objektiewe funksie van hierdie vraestel is relatief eenvoudig, dit is, die totale massa van die struktuur. Die doel van optimalisering is om die totale massa van die struktuur te verminder. Volgens die resultate van eindige element-analise van elke werkstoestand, in die vyf werksomstandighede, die graad van gevaar neem af van werkende toestand 25 tot werkende toestand 78 en uiteindelik tot werkende toestand 87. Ter wille van omsigtigheid, hierdie vraestel kies die gevaarlikste werkstoestand (werkende toestand 25) as die optimalisering werkstoestand. Onder hierdie werkende toestand, die optimeringsresultaat sal maak dat die struktuur geneig is om veiliger te wees.

2.4   Stel die optimaliseringsalgoritme op
Die ANSYS-optimeringsalgoritme omskep die beperkte optimaliseringsprobleem in 'n onbeperkte optimaliseringsprobleem deur die doelfunksie te benader of 'n straffunksie by die doelfunksie te voeg. Daar is gewoonlik twee tipes algoritmes, nul-orde algoritme en eerste-orde algoritme [3]. Die nul-orde algoritme word ook die direkte metode genoem, wat nie die eerste-orde gedeeltelike afgeleide inligting gebruik nie. Die eerste-orde algoritme word ook die indirekte metode genoem, wat die eerste-orde gedeeltelike afgeleide inligting gebruik. Oor die algemeen, die eerste-orde algoritme het 'n groot hoeveelheid berekening en 'n hoë akkuraatheid van die berekeningsresultaat, terwyl die nul-orde algoritme 'n klein hoeveelheid berekening het, 'n vinnige werkingspoed, en 'n lae akkuraatheid van die resultaat, maar dit kan basies die meeste projekte oplos. Hierdie vraestel kies die nul-orde algoritme. Die nul-orde algoritme pas by die responsfunksie van die ontwerpveranderlikes, toestand veranderlikes, en objektiewe funksies gebaseer op 'n sekere aantal steekproewe, en soek dan die optimale oplossing. Hierdie vraestel stel die lusbeheerparameter op 50. Na die opstel van die ontwerp veranderlikes, beperkings, objektiewe funksies, optimaliseringsalgoritmes en ander parameters, iteratiewe optimalisering word uitgevoer, en die optimaliseringsresultate word uiteindelik verkry, soos in tabel getoon 1. Volgens tabel 1, onder die uitgangspunt om aan die sterktekriterium te voldoen, die totale massa van die struktuur word tot ongeveer 25t verminder, met 'n vermindering van tot 30%.

3.5 Strukturele optimalisering ontwerp idees

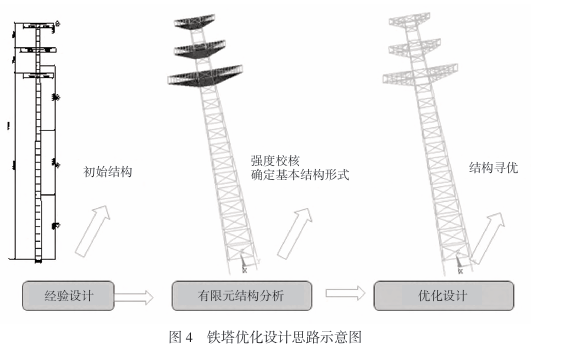
Van bogenoemde strukturele eindige element analise tot strukturele optimeringsontwerp, 'n universele idee kan opgesom word. Die eerste stap is om die aanvanklike ontwerpskema deur empiriese ontwerp te verkry. Volgens die toringontwerpvereistes en ontwerpvoorwaardes, die basiese strukturele vorm en basiese parameters van die transmissietoring word eers op grond van ervaring bepaal. Die rasionaliteit van die aanvanklike ontwerpskema hang af van die ontwerpervaring van die ontwerper. Die tweede stap is om eindige element-analise te gebruik om die sterkte te kontroleer. Verbeter die onredelike dele wat in die aanvanklike ontwerpskema kan bestaan. Die derde stap is strukturele optimeringsontwerp, en vind die optimale struktuur onder die veronderstelling om aan die beperkings te voldoen. Die skematiese diagram van hierdie optimaliseringsidee word in Figuur getoon 4. Die tradisionele “voorlopige ontwerp-analise en verifikasie-terugwysiging-analise en verifikasie” empiriese ontwerpmetode is ondoeltreffend, tydrowend, en die struktuur kan oorbodig en onekonomies wees. Die idee van optimaliseringsontwerp wat in hierdie vraestel voorgestel word, neem empiriese ontwerp as die oorspronklike basis, gee volle spel aan die subjektiewe kreatiwiteit en ontwerpervaring van ontwerpers, en is gebaseer op eindige element simulasie analise en optimalisering. Dit gebruik moderne optimeringsalgoritmes en gebruik die kragtige rekenaarkrag van rekenaars om iteratiewe analise uit te voer. Dit kan die mees geoptimaliseerde struktuur in 'n korter tyd vind, verbeter die ontwerpdoeltreffendheid aansienlik, optimaliseer die ontwerpresultate, bespaar tyd en hulpbronkoste, en het goeie ekonomiese voordele.

3 Gevolgtrekking

Hierdie vraestel stel 'n eindige element analise model van 'n transmissietoring daar (vier-buis toring), gebaseer op watter eindige element analise en strukturele optimeringsontwerp uitgevoer word, en uiteindelik word 'n verwysingsontwerpskema verkry. Die eindige element model is gebaseer op die APDL taal, realiseer parametriese beheer, het 'n hoë mate van outomatisering, en kan by verskillende toringhoogtes aanpas, dwarsbalk posisies, kruisarm posisies, verskeie deursnitparameters en materiaalparameters van toringtipes, die verskaffing van 'n verwysing vir die ontleding van soortgelyke strukture in die toekoms. Daarbenewens, hierdie vraestel stel ook 'n algemene idee van toringontwerp voor, naamlik, empiriese ontwerp - eindige element strukturele analise - optimalisering ontwerp, wat ontwerpdoeltreffendheid verbeter en koste bespaar, en kan 'n verwysing verskaf vir die oplossing van soortgelyke ingenieursprobleme.